다익스트라 알고리즘

1. 개요

다익스트라 알고리즘은, 그래프 상의 한 vertex에서 다른 vertex들에 대해 최단거리를 계산하는 알고리즘이다. BFS 역시 그래프상에서 최단거리를 구하는데 활용할수 있지만, 각 edge에 가중치가 있는 경우 다익스트라 알고리즘등의 다른 방법을 사용해야 한다.

2. 주의사항

음의 가중치가 있는 경우 사용할수 없다. 다익스트라 알고리즘의 경우 구현방법이 다익스트라님이 구현한 O(V^2) 의 방법과 우선순위큐를 사용한 O((V + E)logV 방법이 존재하므로 시간복잡도가 적은 방법으로 구현하는것이 좋다.

3. O(V^2)

def solution(N, edges, K):
    dists = [10000000 for _ in range(N + 1)]
    
		# 시작점
		dists[1] = 0
    
    for _ in range(N):
        for edge in edges:
            i, j, dist = edge
            if dists[i] > dists[j] + dist: dists[i] = dists[j] + dist
            if dists[j] > dists[i] + dist: dists[j] = dists[i] + dist
   
    return dists

vertex의 갯수만큼 edge들에 대해 최단거리를 갱신한다. 알고리즘의 구현과정이 간단하지만 시간복잡도가 높은 단점이 있다.

O((V + E)logV)

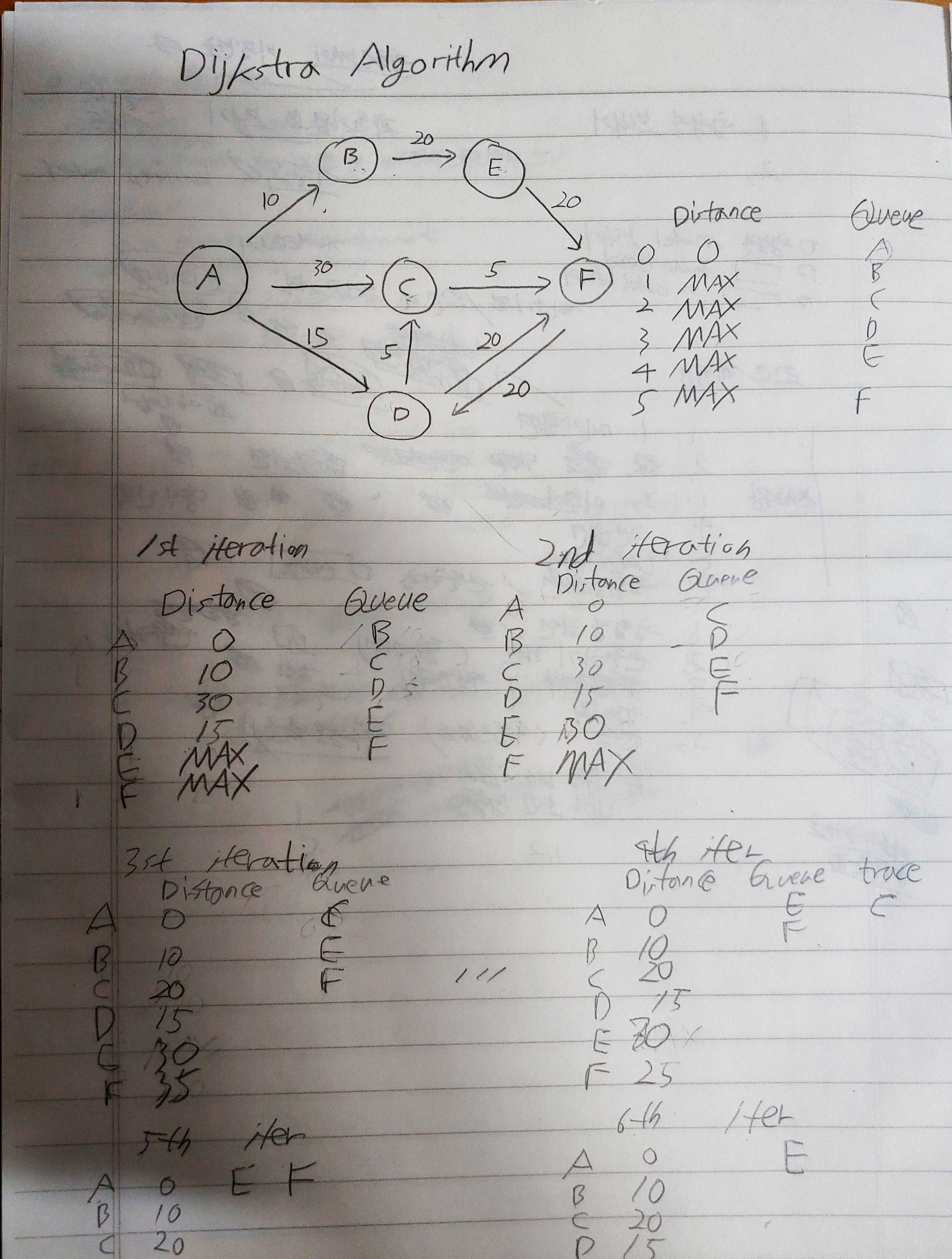
가장 최단거리의 노드순으로 연결되어있는 노드들을 검사하여 최단거리를 갱신한다. 노드를 검사한후 다음 노드를 결정할때 최단거리인 노드를 선택해야 하므로 우선순위큐의 도움을 받았다.

노드에 대한 검사가 끝나면 해쉬 테이블에 집어 넣어서, 향후 같은 노드를 검사하지 않도록 방지해주었다.

def solution(N, road, K):
    dists, dists[1] = [10000000 for _ in range(N + 1)], 0
    is_traced = set()
    graph, queue = [[] for _ in range(N + 1)], [(0, 1)]
    
    for (i, j, d) in road:
        graph[i].append((j, d))
        graph[j].append((i, d))

    while queue:
        v_dist, v = heapq.heappop(queue)

        if v in is_traced: continue
            
        is_traced.add(v)

        for (dest, dist) in graph[v]:
            candid_dist = v_dist + dist
            if candid_dist < dists[dest]:
                dists[dest] = candid_dist
                heapq.heappush(queue, (candid_dist, dest))