카카오코드 2017, 리틀프렌즈사천성, java
1. 문제 출처
2. Introduction
카카오코드 2017 본선에 출제되었던 문제이다. 여러가지 풀이방법이 있지만 이글에서는 DFS를 활용한 풀이를 다뤄보고자 한다. 상당히 어려웠는데 풀다보니 뿌듯함(?)을 느낄수 있었다.
3. 타일을 위한 자료구조 + 어떤 순서로 타일을 제거할것인가?
각각의 타일당 2개씩 board에 존재하므로, board에 위치한 타일의 행, 열을 파악해놓으면 탐색을 할때 편리할것 같았다. 그래서 HashMap 자료구조를 활용해 board를 탐색하면서 타일이 존재하는 행, 열 정보를 저장하였다.
또한 dfs를 위해서는 graph의 구축이 필요하기 때문에 board를 char[][] 배열로 변환하여 graph로 활용하고 이때 타일을 제거하면, 값을 ‘.’로 바꿔주어 다른 타일들을 제거할수 있도록 하기로 생각했다.
생각같아선 아무순서로 제거하고 싶지만 문제의 조건에 답이 여러가지인 경우 알파벳순서로 반환하도록 해야하는 조건이 있다. 따라서 어떤 타일들이 존재하는지 파악해야하고, 이를 정렬해놓으면 문제해결에 도움을 얻을수 있다. 이를 위해 board를 검사하면서 Set 자료구조에 일단 모든 타일을 넣었고, 이를 리스트로 변환하여 정렬후 문제해결에 사용했다.
private final int MAX_WIDTH = 100;
private Map<Character, List<int[]>> db = new HashMap<>();
private List<Character> keys;
private char[][] graph = new char[MAX_WIDTH][MAX_WIDTH];
private void init(int m, int n, String[] board) {
Set<Character> nodes = new HashSet();
for(int i = 0; i < m; ++i) {
for(int j = 0; j < n; ++j) {
char key = board[i].charAt(j);
graph[i][j] = key;
if(key == '*' || key == '.') continue;
if(!db.containsKey(key))
db.put(key, new ArrayList(2));
db.get(key).add(new int[] {i, j});
nodes.add(key);
}
}
keys = new ArrayList(nodes);
Collections.sort(keys);
}
그리고 정렬된 타일들을 대상으로 검사하여 해당 타일을 제거할수 있는지의 여부를 파악한다. 이때 중요한점은 제거가능한 타일이 존재하면, 해당 타일을 제거한후 정렬된 타일들을 처음부터 다시 검사해야한다. 예를 들어 A, B, C, D의 타일이 존재하는데 A를 제거못햇고, B를 제거했다면 A를 다시 제거할수 있는 가능성이 생기기 때문이다. 이점을 관과하여 테스트를 통과하지 못했다.
private final int MAX_WIDTH = 100;
private Map<Character, List<int[]>> db = new HashMap<>();
private List<Character> keys;
private char[][] graph = new char[MAX_WIDTH][MAX_WIDTH];
private boolean pung() {
while(!keys.isEmpty()) {
ListIterator<Character> it = keys.listIterator();
Character punged_key = null;
Integer punged_key_index = null;
while(it.hasNext()) {
int key_index = it.nextIndex();
char key = it.next();
if(pungable(key)) {
// 제거할수 있으면 제거할 타일을 설정후 빠져나온다.
// 이전 타일들을 제거할 가능성이 생기기 때문이다.
punged_key_index = key_index;
punged_key = key;
break;
}
}
// 타일들을 전부 검사했는데
// 만약 제거할수 있는 타일이 없으면 "IMPOSSIBLE" 하다
if(punged_key == null) return false;
//반환할 String에 붙여준다.
ans.append(punged_key);
// graph에서 타일을 제거한다. ("."로 설정한다.)
pung(punged_key);
// 제거한 타일을 정렬된 리스트에서 지워준다.
keys.remove(punged_key_index.intValue());
}
return true;
}
4. 어떠한 상황에 타일을 제거할수 있을까?
1. 두 타일이 가로나 세로로 서로 붙어 있는 경우
두타일이 서로 붙어 있다면 바로 제거가 가능하다. 제거한후에는 해당 노드를 ‘.’ 으로 설정하여 다른 타일들이 삭제될수 있도록 해줘야 한다.

private boolean pungable(char key) {
List<int[]> idxs = db.get(key);
int[] idx_s = idxs.get(0), idx_e = idxs.get(1);
int s_i = idx_s[0], s_j = idx_s[1];
int e_i = idx_e[0], e_j = idx_e[1];
/*
* 두노드 사이의 거리가 1이면 삭제할수 있다.
* 행의 경우 끝나는 노드가 더 작은 행에 있을수 있으므로 abs를 사용했다.
*/
if((e_i-s_i + Math.abs(e_j-s_j)) == 1) return true;
...
}
2. 두 타일간에 한번만 꺽어서 도달할수 있는 경우
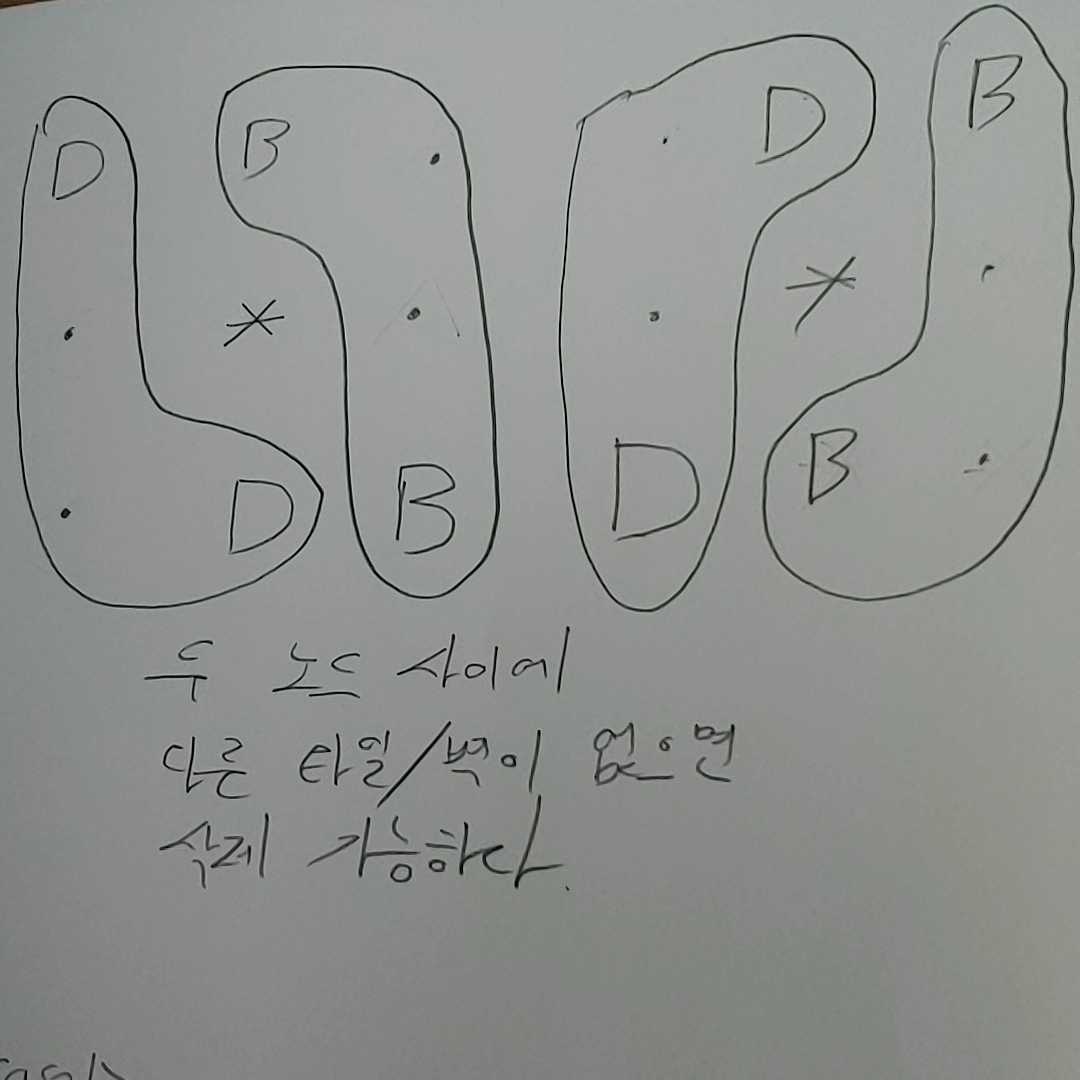
두 타일을 가로세로로 줄을 그으면 ㄱ, ㄴ 이나 이를 좌우 대칭한 형태가 나온다. 이때 거쳐가는 노드들에 다른 타일이 없거나 비어있으면(‘.’) 두 타일을 제거할수 있다.
항상 같은 모양의 타일은 두개가 있으므로 타일들의 이름을 start, end 라고 해보자, 본인은 end가 좀더 뒤의 행에 있는 타일로 잡고 문제를 해결했지만, 뒤에 있는 열로 잡고 해결할수 있다. end의 경우 뒤에 있는 행에 있다 가정하면 열은 앞에 있을수 있고 뒤에 있을수도 있다.
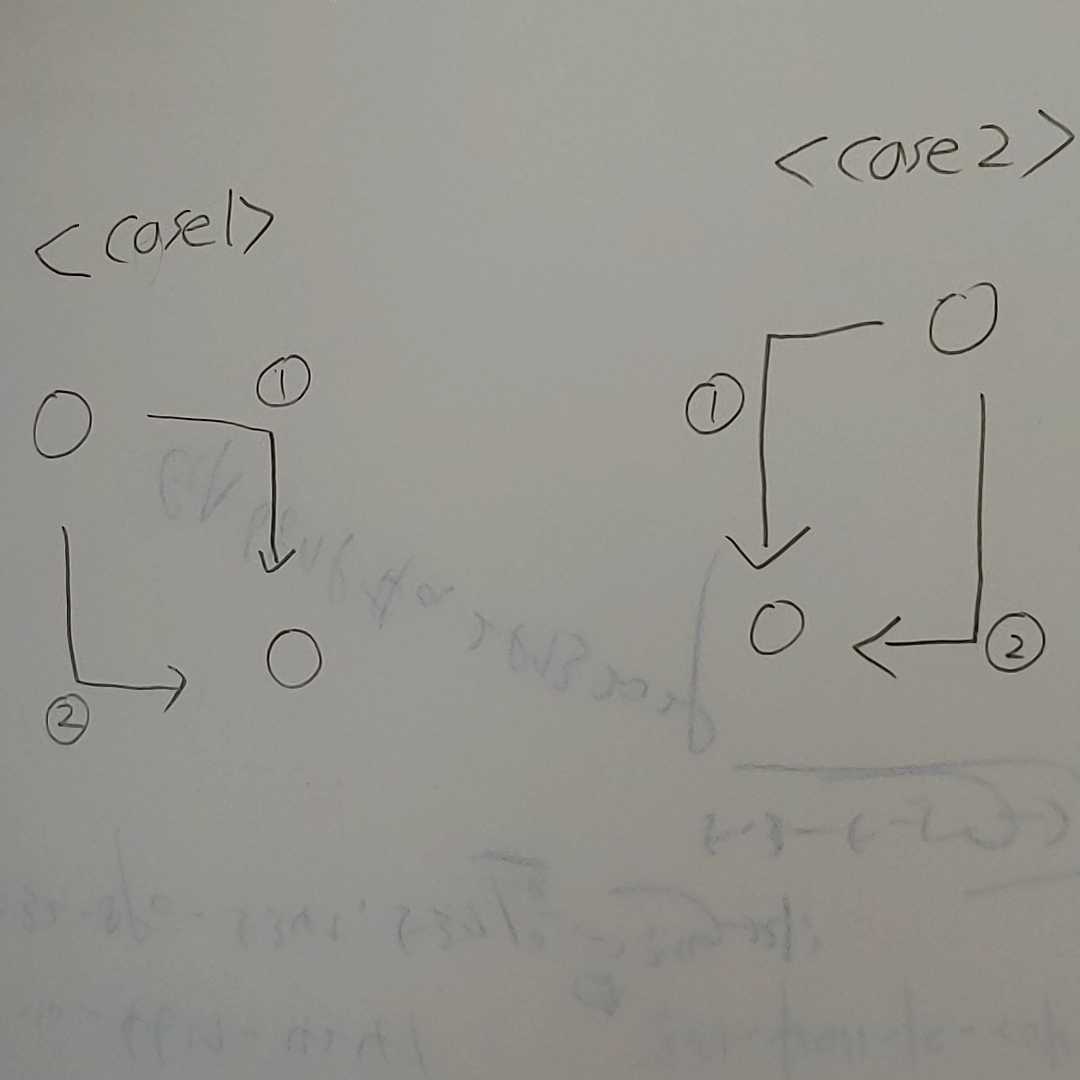
따라서 제거 가능여부를 검사할때 두가지 경우중 하나를 골라 탐색하게 된다. 그리고 각각의 경우마다 end에 도달할수 있는 두가지 경로를 검사하여 삭제여부를 판단하면 된다. 삭제후에는 두노드를 ‘.’ 으로 설정하여 다른 타일들이 삭제될수 있도록 해줘야 한다.
그럼 첫번째 경우인 두타일이 붙어있는 경우와 함께 pungable을 함수를 다음과 같이 수정할수 있다. 만약 end의 열이 start의 행보다 작다면 열을 줄여나가면서 검사하고 그렇지않다면 열을 늘려가면서 검사하면 된다.
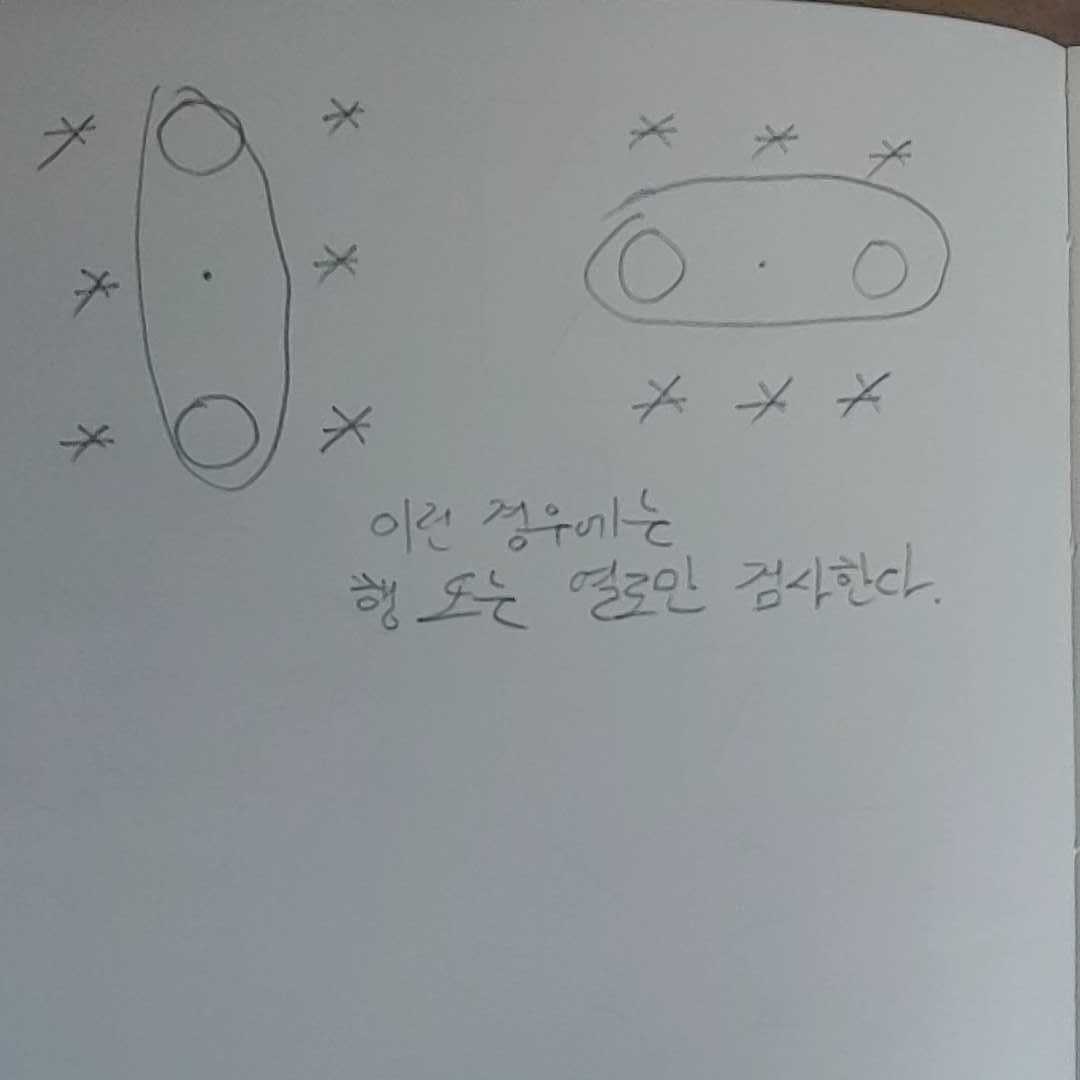
만약에 start와 end의 행이 같다면 열만 검사하고, 열이 같다면 행만 검사하면 된다. 본인은 이를 관과해서 행이 같은상황에서 행을 검사하다 arrayboundexception에 시달렸다. 방어로직을 잘짜면 될것 같기도한데 애초에 검사안하는게 좋은 방법인것 같다.
private boolean pungable(char key) {
List<int[]> idxs = db.get(key);
int[] idx_s = idxs.get(0), idx_e = idxs.get(1);
int s_i = idx_s[0], s_j = idx_s[1];
int e_i = idx_e[0], e_j = idx_e[1];
//case1
if((e_i-s_i + Math.abs(e_j-s_j)) == 1) return true;
//case2 (ㄱ, ㄴ 혹은 좌우대칭된 경로를 검사하기)
// 만약 행이나 열이 같다면 바로 false를 반환하여 하나만 검사하자
boolean row_test = (s_i == e_i ? false :
test(s_i+1, s_j, e_i, e_j, true));
boolean col_test = (s_j == e_j ? false :
test(s_i, s_j < e_j ?
s_j+1:s_j-1, e_i, e_j, false));
return row_test || col_test;
}
아래의 코드가 실제로 정해진 경로에 대해 pung할수 있는지의 여부를 검사하는 dfs 재귀함수 코드이다. 지금 보니깐 투포인터문제랑 비슷한것 같다. 여하튼 is_row라는 boolean 타입 변수로 지금 조정하는것이 행인지 열인지를 나타내려 했다.
행이라면 행을 증가시키고 열이라면 열을 증가시키거나 감소시킨다. 만약 행이나 열이 같아지는 상황이 발생한다면 그때부터 is_row를 반전시키고 열이나 행을 조정하면서 탐색하도록 했다. 탐색하면서 end 타일을 만나게 되면 pungable 하다 말할수 있다. 만약 다른타일이나 벽(‘*‘)을 만나면 pungable하다 말할수 없다.
private boolean pungable(int i, int j,
int e_i, int e_j, boolean is_row) {
if(graph[i][j] == graph[e_i][e_j]) return true;
if(graph[i][j] != '.') return false;
if(is_row) {
return i != e_i ? test(i+1, j, e_i, e_j, true) :
test(i, j<e_j ? j+1:j-1, e_i, e_j, false);
}
else {
return j != e_j ?
test(i, j<e_j ? j+1:j-1, e_i, e_j, false) :
test(i+1, j, e_i, e_j, true);
}
}
5. 시간복잡도 추정
이문제의 조건은 다음과 같다.
1 <= m, n <= 100
board의 원소는 아래 나열된 문자로 구성된 문자열이다. 각 문자의 의미는 다음과 같다.
.: 빈칸을 나타낸다.
*: 막힌 칸을 나타낸다.
알파벳 대문자(A-Z): 타일을 나타낸다. 이 문제에서, 같은 글자로 이루어진 타일은 한 테스트 케이스에 항상 두 개씩만 존재한다.
board에는 알파벳 대문자가 항상 존재한다. 즉, 타일이 없는 입력은 주어지지 않는다.
최대 타일의 수를 n이라고 하자, 매 iteration마다 최악의 경우로 타일이 1나씩만 제거된다고 가정해보자. 그리고 각각의 타일종류마다 board에 두개의 타일이 박혀있고 삭제여부를 판단하기 위해 board를 탐색하기 위해서는 최악의 경우 K = (100 + 100) * 2 - 4번 검사하게 된다. 이때 시간복잡도를 계산하면 다음과 같다.
check_tiles = K * (n + (n-1) + (n-1) ... + 1) = K * n * (n+1) / 2
O(n) = n^2
이문제의 경우 타일의 수는 알파뱃의 숫자로 한정되어있으므로 (26 * 26) 시간초과없이 문제를 해결할수 있을것으로 추정한다. 하지만 타일의 수가 많다면 다른 풀이 방법을 고심해봐야 할것 같다.
6. 전체코드
import java.util.HashMap;
import java.util.Map;
import java.util.HashSet;
import java.util.Set;
import java.util.List;
import java.util.ArrayList;
import java.util.Collections;
import java.util.ListIterator;
class Solution {
private final int MAX_WIDTH = 100;
private Map<Character, List<int[]>> db = new HashMap<>();
private List<Character> keys;
private char[][] graph = new char[MAX_WIDTH][MAX_WIDTH];
private StringBuilder ans = new StringBuilder();
public String solution(int m, int n, String[] board) {
init(m, n, board);
return pung() ? ans.toString() : "IMPOSSIBLE";
}
private void init(int m, int n, String[] board) {
Set<Character> nodes = new HashSet();
for(int i = 0; i < m; ++i) {
for(int j = 0; j < n; ++j) {
char key = board[i].charAt(j);
graph[i][j] = key;
if(key == '*' || key == '.') continue;
if(!db.containsKey(key))
db.put(key, new ArrayList(2));
db.get(key).add(new int[] {i, j});
nodes.add(key);
}
}
keys = new ArrayList(nodes);
Collections.sort(keys);
}
private boolean pung() {
while(!keys.isEmpty()) {
ListIterator<Character> it = keys.listIterator();
Character punged_key = null;
Integer punged_key_index = null;
while(it.hasNext()) {
int key_index = it.nextIndex();
char key = it.next();
if(pungable(key)) {
punged_key_index = key_index;
punged_key = key;
break;
}
}
if(punged_key == null) return false;
ans.append(punged_key);
pung(punged_key);
keys.remove(punged_key_index.intValue());
}
return true;
}
private boolean pungable(char key) {
List<int[]> idxs = db.get(key);
int[] idx_s = idxs.get(0), idx_e = idxs.get(1);
int s_i = idx_s[0], s_j = idx_s[1];
int e_i = idx_e[0], e_j = idx_e[1];
if((e_i-s_i + Math.abs(e_j-s_j)) == 1) return true;
boolean row_test = (s_i == e_i ? false :
pungable(s_i+1, s_j, e_i, e_j, true));
boolean col_test = (s_j == e_j ? false :
pungable(s_i, s_j < e_j ?
s_j+1:s_j-1, e_i, e_j, false));
return row_test || col_test;
}
private boolean pungable(int i, int j,
int e_i, int e_j, boolean is_row) {
if(graph[i][j] == graph[e_i][e_j]) return true;
if(graph[i][j] != '.') return false;
if(is_row) {
return i != e_i ? pungable(i+1, j, e_i, e_j, true) :
pungable(i, j<e_j ? j+1:j-1, e_i, e_j, false);
}
else {
return j != e_j ?
pungable(i, j<e_j ? j+1:j-1, e_i, e_j, false) :
pungable(i+1, j, e_i, e_j, true);
}
}
private void pung(char key) {
List<int[]> idxs = db.get(key);
int[] idx_s = idxs.get(0), idx_e = idxs.get(1);
int s_i = idx_s[0], s_j = idx_s[1];
int e_i = idx_e[0], e_j = idx_e[1];
graph[s_i][s_j] = '.';
graph[e_i][e_j] = '.';
}
}

Leave a comment