카카오 인턴쉽 2020, 경주로 건설, python

1. 문제 출처

문제 바로 가기

2. Introduction

카카오인턴쉽 2020에 출제되었던 문제이다. BFS를 활용하면 풀수가 있는데 DP의 요소가 녹아들어있는(?) 나에게는 까다로운 문제였다.

3. 직선도로와 간선도로 비용 계산

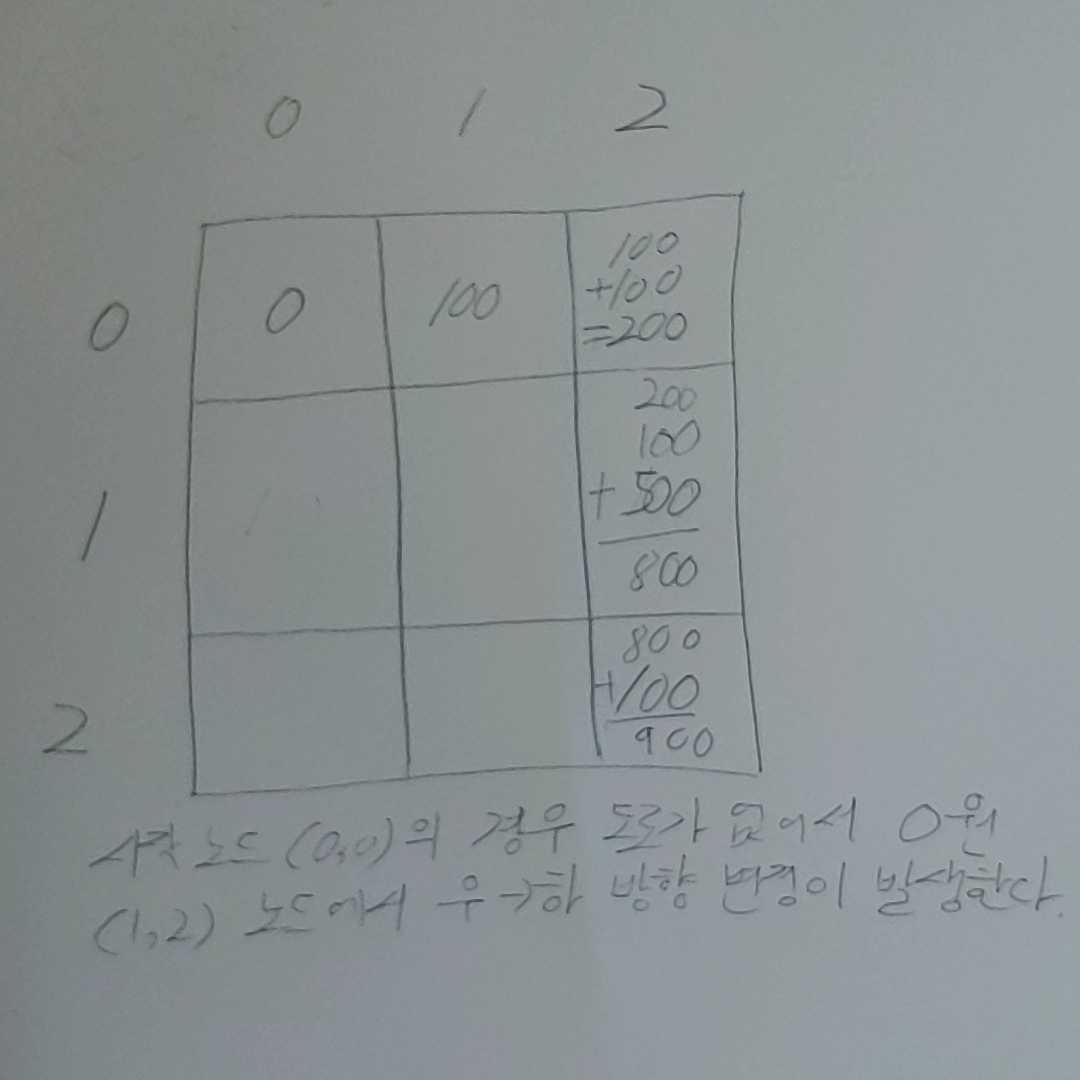
시작노드에서 도착노드에 도로를 건설할때 100원의 비용이 발생하게 된다. 이때 도로를 설치하는 방향은 상, 하, 좌, 우로 설치할수 있다. 만약에 최근 설치한 방향과 다른 방향으로 도로를 건설하게 되면 비용이 500원의 추가비용이 발생한다. 3x3 배열에서 ㄱ형태로 도로를 설치했을때 발생되는 비용은 100 * 4 + 500 = 900원이 발생하게 된다. 맨 처음 도로를 깔때는 우, 하 방향으로 진행을 하게 되는데 이때 발생되는 비용은 무조건 100원이다. 따라서 본인은 일단 방향이 바뀌는것으로 간주하여 600원으로 계산한다음, 나중에 답을 반환할때 500원을 빼서 반환하는 트릭을 사용했다.

N, Q = len(board), deque([(0,0,-1,0)])

while Q:
    # yx좌표, 방향, 비용
    # 상하좌우는 0, 1, 2, 3으로 나타내었으므로, 맨 처음 진행할때는 -1과 달라서 무조건 600이 된다.
    y, x, d, c = Q.pop()
    ......
# 따라서 답을 반환할때 500을 빼준다.
return min(dists[-1][-1]) - 500

4. 각 노드의 최소비용은 갱신될수 있다.

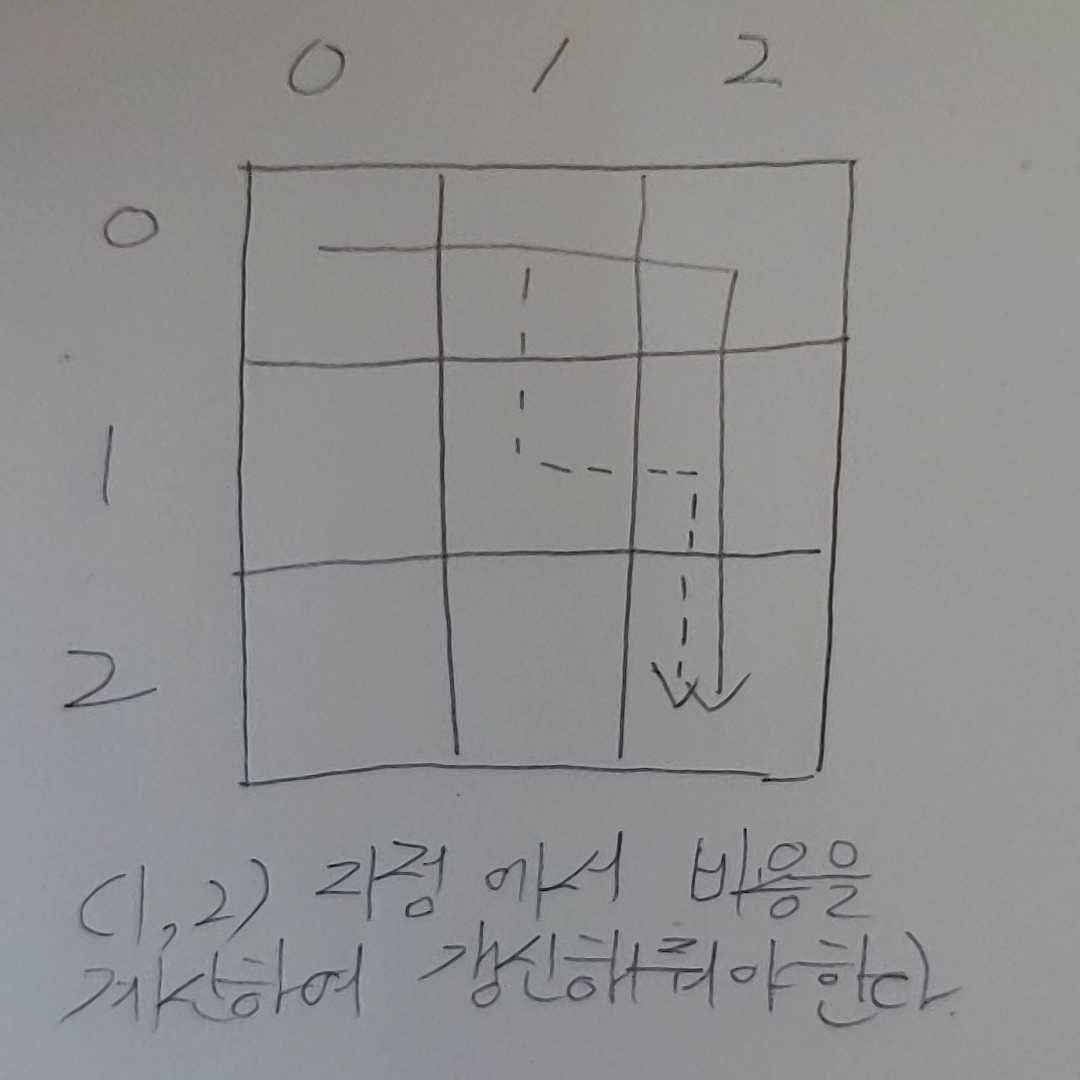
기존의 BFS의 알고리즘의 경우, 방문했던 노드를 따로 저장해 놓았다가 향후 다시 노드를 방문하고자 할때 재방문을 막아 무한루프를 막는다. 하지만 이문제의 경우 규칙을 그대로 적용할수 없다. 노드에서 계산된 최소비용이 갱신될 가능성이 있기 때문이다. 따라서 방문했던 노드들에 계산했던 비용을 저장하되, 다시 탐색했을때 비용이 적으면 비용을 갱신하고 다시 방문해줘야 한다.

5. 각 노드마다 4가지 방향이 존재할수 있다.

앞에서 한번 설명했지만, 노드에 도로를 깔수있는 방향은 4가지 방향이다. 문제는 노드에 계산된 비용을 하나로만 관리하면 최종적으로 계산된답이 최소값이 아닐 가능성이 존재한다. 문제의 경우 모든 노드에 도로를 깔수 있는 이상적인 상황이 아니다. 만약 최소비용으로 깔았을때 같은 방향의 다음 노드가 벽이라면 진행이 안되거나 방향을 틀어야 한다.

이때 계산된 비용은 최솟값이라 보장할수 없기때문에 최소비용은 아니지만 방향이 다르다면 다시 재탐색을 해야할 필요성이 생긴다. 따라서 각 노드마다 4가지 방향으로 도로를 깔았을때의 비용을 각각 저장하고, 모든 탐색이 끝난후 최종노드 (n, n)에서 4가지 방향으로 계산된 값들중 최솟값을 반환하면 된다.

dists = [[[MAX_DIST for _ in range(4)] for _ in range(N)] for _ in range(N)]

6. 전체코드

from collections import deque

def solution(board):
    N, Q = len(board), deque([(0,0,-1,0)])
    MAX_DIST = 100000000
    OUTBOUNDS, UNREACHABLE = (N, -1), 1
    
    dists = [[[MAX_DIST for _ in range(4)]
        for _ in range(N)] for _ in range(N)]
    
    while Q:
        y, x, d, c = Q.pop()

        if (y, x) == (N-1, N-1): continue

        cases = [(y, x-1), (y, x+1), (y-1, x), (y+1, x)]
        for direction, (ny, nx) in enumerate(cases):            
            if ny in OUTBOUNDS or nx in OUTBOUNDS: continue
            if board[ny][nx] == UNREACHABLE: continue

            cost = c + (100 if d == direction else 600)
    
            if dists[ny][nx][direction] <= cost: continue
                
            Q.appendleft((ny, nx, direction, cost))
            dists[ny][nx][direction] = cost

    return min(dists[-1][-1]) - 500